Why Does Theory Matter in Computer Science? /
Why Does Theory Matter in Computer Science? (Part 1)
Introduction and Big Ideas: Abstraction and Generalization
This is the first installment in the written version of my talk about why I think theory matters in computer science. The talk is quite long, so I thought it would make sense to break it up into a few parts. This section is the most important and contains a lot of the big ideas I illustrate later in the talk! You can find part 2 here, part 3 here, part 4 here, and a list of references here. The entire series is archived here.
Introduction
If you’re a computer science student, you probably had to take an introductory discrete math course at some point. Did you enjoy it? If so, this talk probably isn’t for you, so you can feel free to skip the rest. (Or not – hopefully you feel like you can still learn something from me!)
Jokes aside, it’s actually okay not to enjoy your intro to discrete math course: like, personally, I loved mine, but I also completely hated my discrete probability course and would prefer never to see it again. But I pick on discrete math because I feel like if it’s taught well, it can be a turning point for many people, and it certainly was for me.

Let’s imagine for a second that everyone falls on this sort of spectrum. On one side, we have people who only care about applications, and on the other side, we have people who only care about theory.

Before I took discrete math, and especially during high school, I fell on the “only cares about applications” side of the spectrum. I knew math was useful, but I didn’t care about it. Actually, I hated it and viewed it as necessary suffering. I went into an engineering program straight after high school, and engineering degrees are all about applications. I only wanted to learn math that I could see a concrete use for, and I was fully planning on never taking a math course again after fulfilling my requirements.
I ended up switching to a computer science degree almost by accident (it’s a long story), and discrete math was certainly the course that opened my eyes to what math really is, why we care about it, and how we can use it to solve problems. After finishing the course, I felt as though the entire field of math had been completely misrepresented to me, and I had a much better understanding of why people study math and how it can be useful in and of itself.
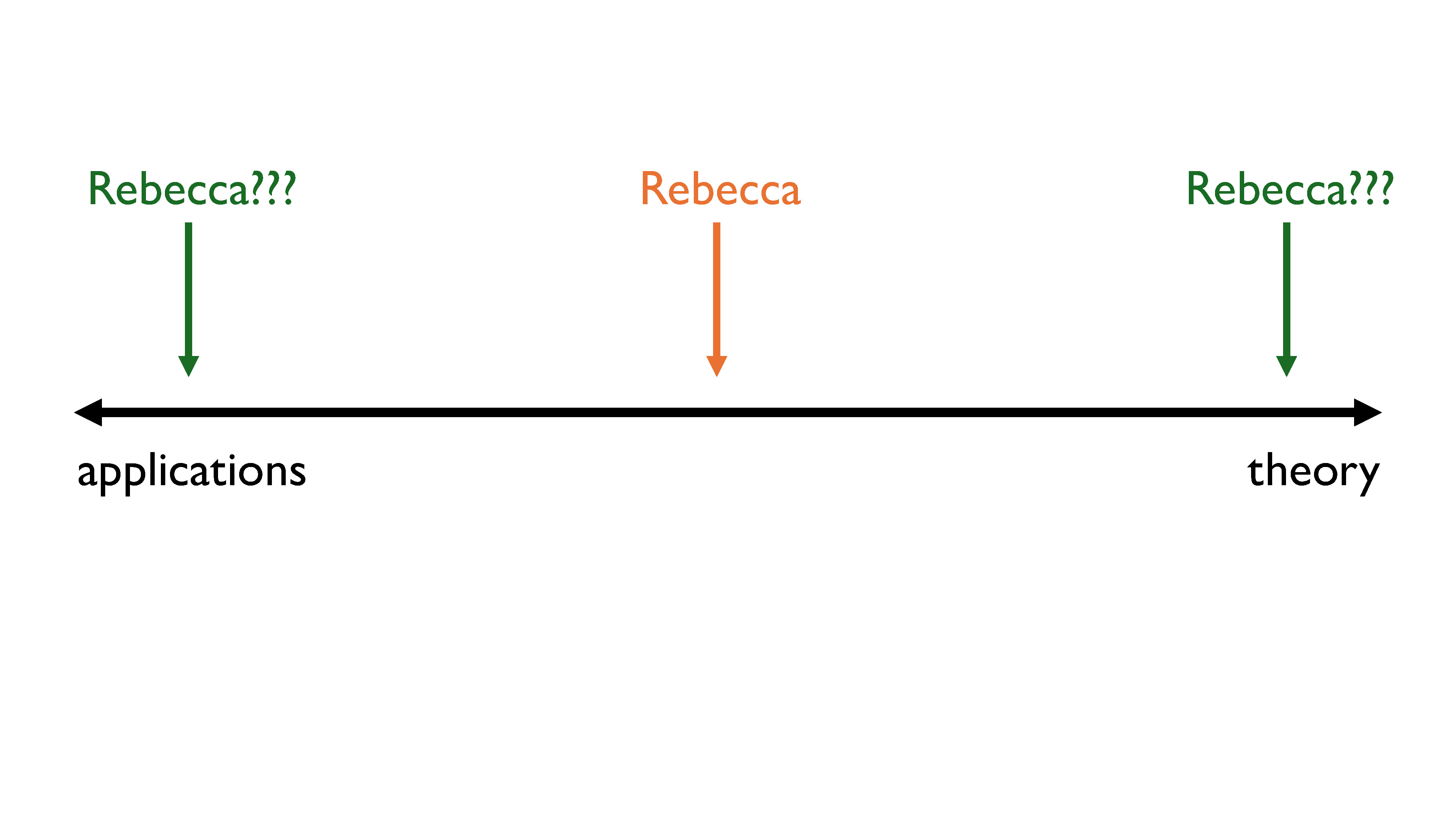
And now I keep taking all these math courses, people keep thinking I’m a math student (which is kind of insane – have you ever met real math students??) and I have a much greater appreciation for theoretical approaches than I used to. Nowadays, I fall more in the middle of this chart, and I think I’ve mostly settled there… with a few wild pendulum swings back and forth.
But that chart is actually a lie.
Theory vs. Applications

Theory and applications are not separate from each other, so we can start to place courses, professions, and different people’s interests on a two axis chart that looks a lot more like this.
In the bottom left corner, we have things that have no practical or theoretical value. If you’re doing one of those things in a professional or academic context, you should just stop, because it’s stupid and useless and no one is going to care about it. In the top right corner, we have things that have both high theoretical value and high practical value. And again, there are probably very few people who are doing things like that, because most people have more of an inclination towards one of theory or application, both in terms of ability and in terms of interest.
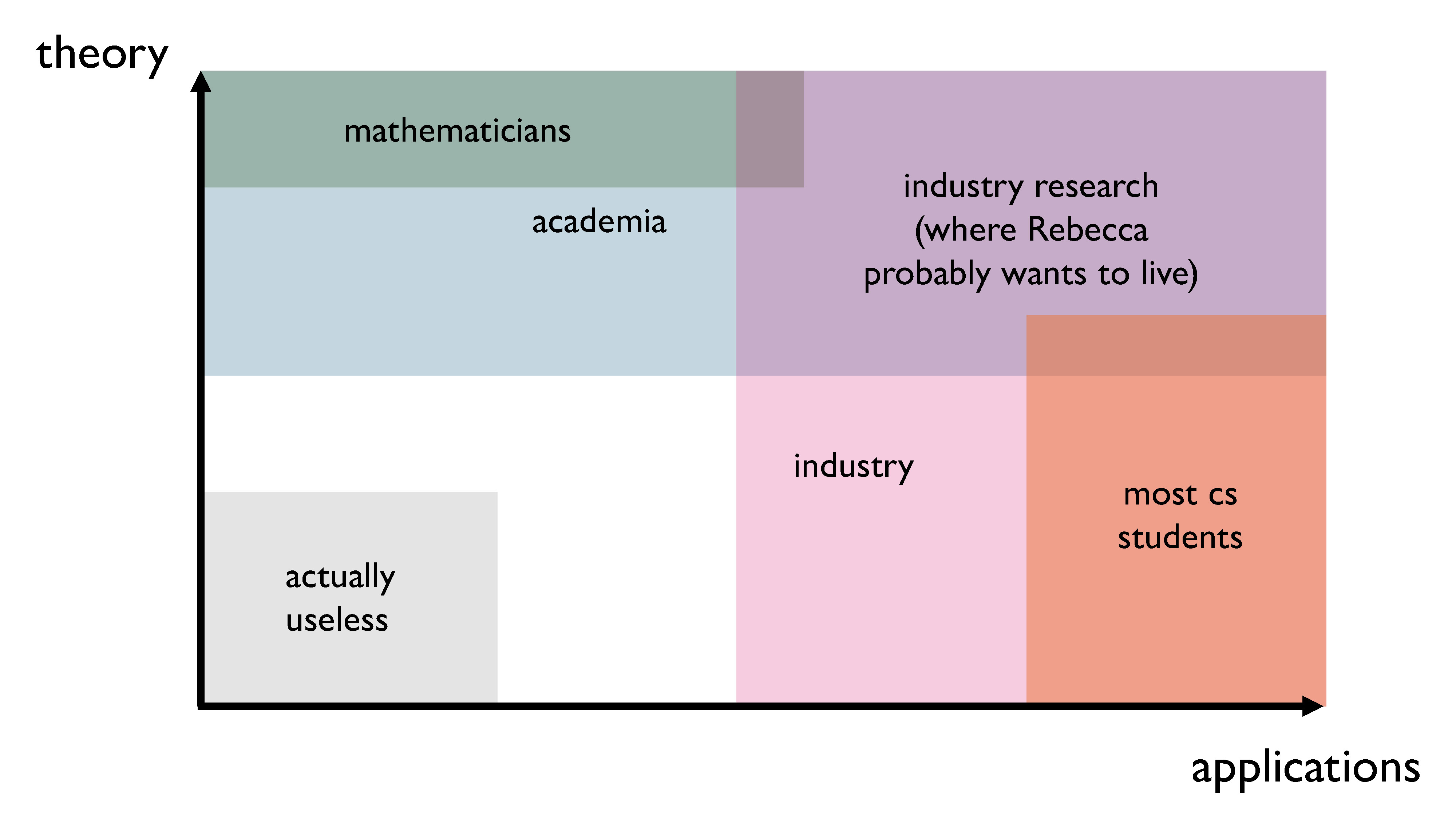
In academia, most people fall into the top half of the chart, because all research involves a theoretical framework and approach. Some of the research may have practical applications, sure, but what academia really values is trying to further knowledge in some way, which usually involves having a firm grounding in theory, or even proposing new ideas and methods. (You’ll notice that pure mathematicians are like, way over in the top left). In industry, most people fall into the right half of the chart, because getting concrete results that are actually useful to the business is of utmost importance. In the intersection of the two areas is where you find industry research, which is where I think I might want to live.
I think most students in computer science programs fall somewhere in the bottom right corner of the chart. We can start to place some different CS courses on this chart, and get a better sense of what the theory/applications split actually looks like in a CS degree. I’ve put a few of the courses I’ve taken on the slide that follows, in the places where I think they actually belong.
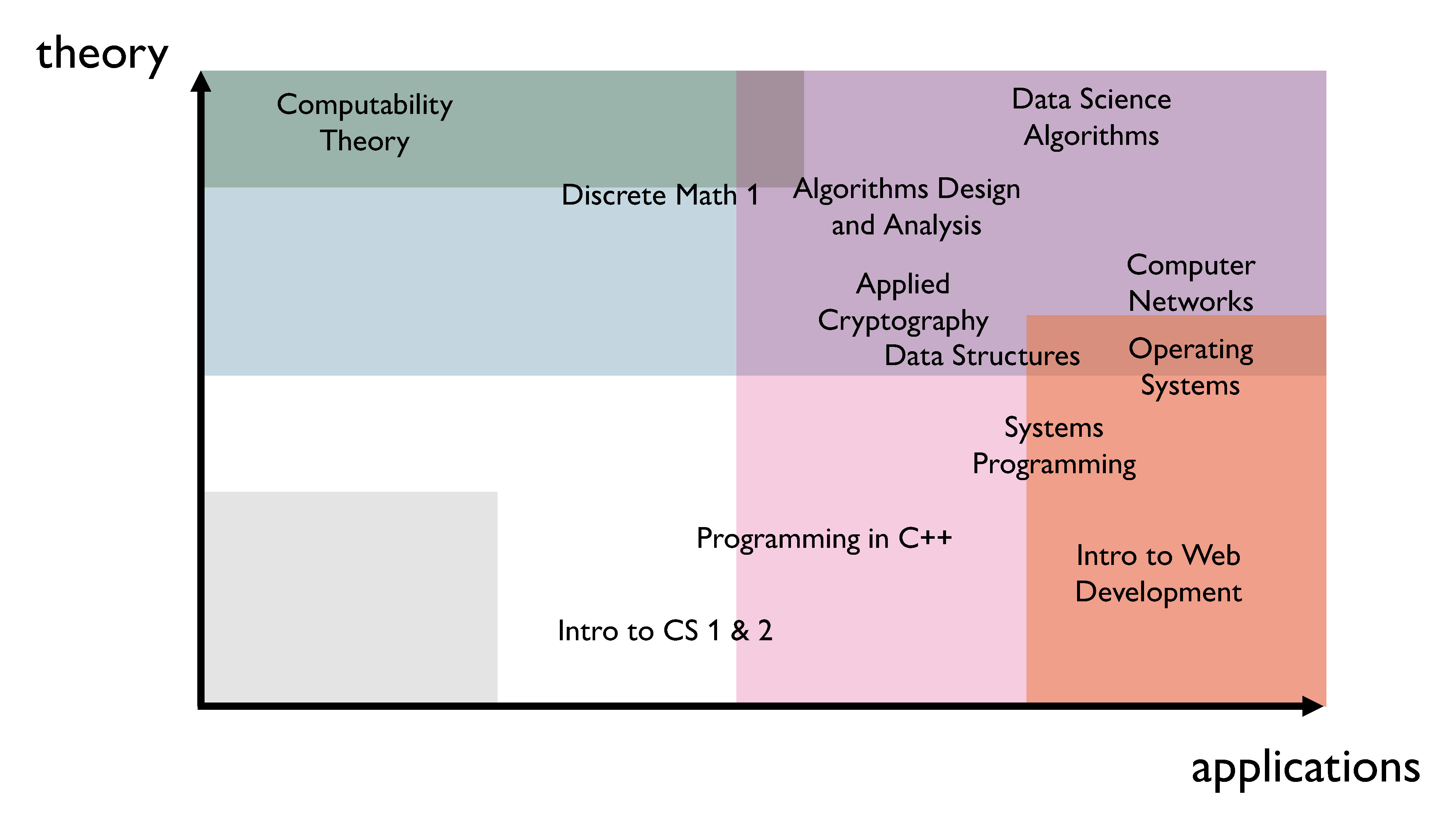
You should take this chart with a grain of salt – it’s really just my opinion. But as we can see, computer science degrees are very applied. However, as we get further into the degree, the theoretical component also steadily increases. In a lot of cases, it’s very difficult to fully decouple theory from applications, and doing so can actually be a terrible idea.
My goal isn’t to convince you to become a theorist, and especially not a pure theorist. There are other people out there with that goal: we call them math professors, and you should totally stay away from them. (Just kidding. Sort of.) But my goal is to help you understand why our degree forces us to take theory courses, especially the more math heavy courses, and also to maybe try to convince you that math can be interesting, because math courses aren’t always particularly convincing.
Disclaimers
I should probably mention that some of this is just my opinion, filtered through my experiences and worldview. That’s my disclaimer for the day: please take whatever I say with a grain of salt.
Also, I am not an expert. (Yet.)
WTF is “theory”?
So what do I mean when I say the word “theory”? I should probably get that out of the way first.
Dictionary definitions
Here’s a definition from Merriam Webster. I’m cherry-picking the points that I like and think are relevant here. (Here’s the full definition.) So we have:

- a plausible or scientifically acceptable general principle or body of principles offered to explain phenomena
- a belief, policy, or procedure proposed or followed as the basis of action (here we can think of the scientific method as being a kind of theory, or a theoretical framework)
- the analysis of a set of facts in their relation to one another
I’m also going to show this other definition of theory from the Oxford Learner’s Dictionary. Again, I’m cherry-picking. (Full definition here.)

- a formal set of ideas that is intended to explain why something happens or exists
In summary, according to the two dictionaries, theory helps us understand where methods come from, why different phenomena occur, and how different ideas are related to each other. Theory is also a method for studying these ideas and phenomena.
That being said, I’d like to give my own slightly different definition, which I think will be more relevant for our purposes.

In the context of computer science, I like to think of theory as being something that gives us language for discussing different problems, frameworks for sorting them into different categories, and ideas for finding common ways of solving problems of a certain type.
Abstraction and Generalization
Two common tools that we often use in computer science are abstraction and generalization.

Abstraction is sort of like simplification: it’s stripping away unnecessary details so that the bigger picture becomes more clear. As we iteratively do this over time, the new abstraction might start to look really different from the thing we were originally describing, but the key is that the core idea is still captured – a person looking only at the abstraction should not feel like they’re missing crucial information.
Generalization is related, but slightly different: it allows us to classify larger and larger groups of objects by looking at ways in which they’re fundamentally the same. It can be an iterative process, in the sense that we can build classes that are contained within each other, and it’s not a unique process, in the sense that we can have classes that overlap with each other in different ways, and that there may be multiple ways to build classifications of the objects.
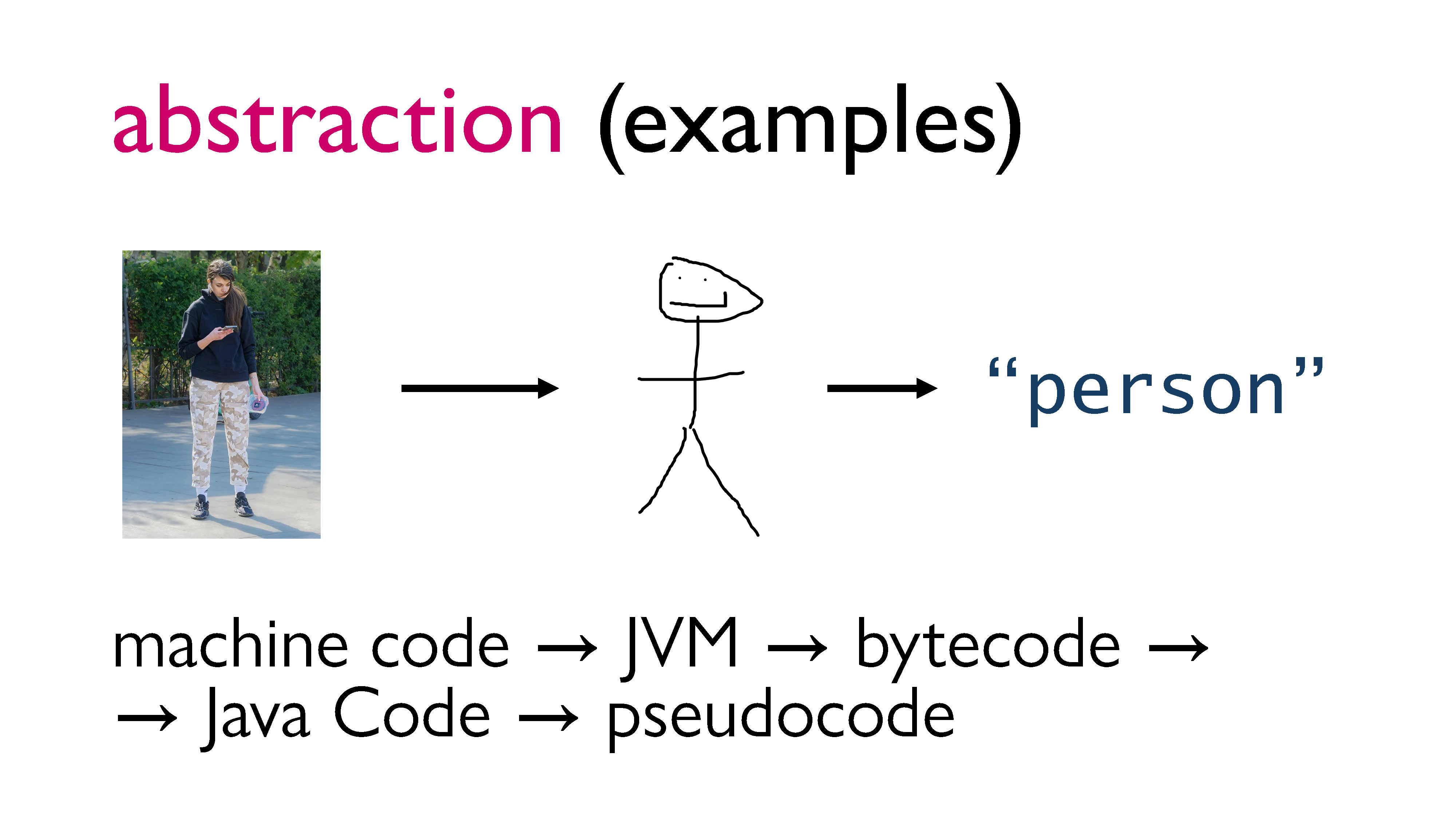
One example of abstraction is the evolution of language. We went from actually drawing things when we wanted to convey them, to using pictograms, to writing words that don’t even look like the original concept. So if I want you to think about the abstract idea of a person, I can show you a real person! But I could also show you a semi-realistic drawing, or a stick figure, or even just the word “person”, and you would still be able to hold the idea of a person in your head, even if the word “person” looks nothing like a human.
But we also do this sort of abstraction in programming all the time. You might have an idea for a program that you can describe using pseudocode, which is pretty abstract but captures the idea. Let’s say you hand off your pseudocode to a colleague to implement in Java. While your colleague is able to understand the program, they will need to add more details so that the computer can interpret it. If they want to then run the program, they will have to compile it first. The compiler will convert the program to bytecode, which will have more specific instructions for the Java Virtual Machine (JVM). When the bytecode is run on the JVM, it will be interpreted into machine code, which will have hardware dependent instructions. And as the code gets executed on the machine, it’ll go down the ladder of abstraction until it hits the level of logic gates that are being turned on and off.
As the original writer of the pseudocode, you don’t need to understand bytecode or machine code or logic gates. You probably don’t even need to know how to write code in Java! This is the beauty of abstraction.
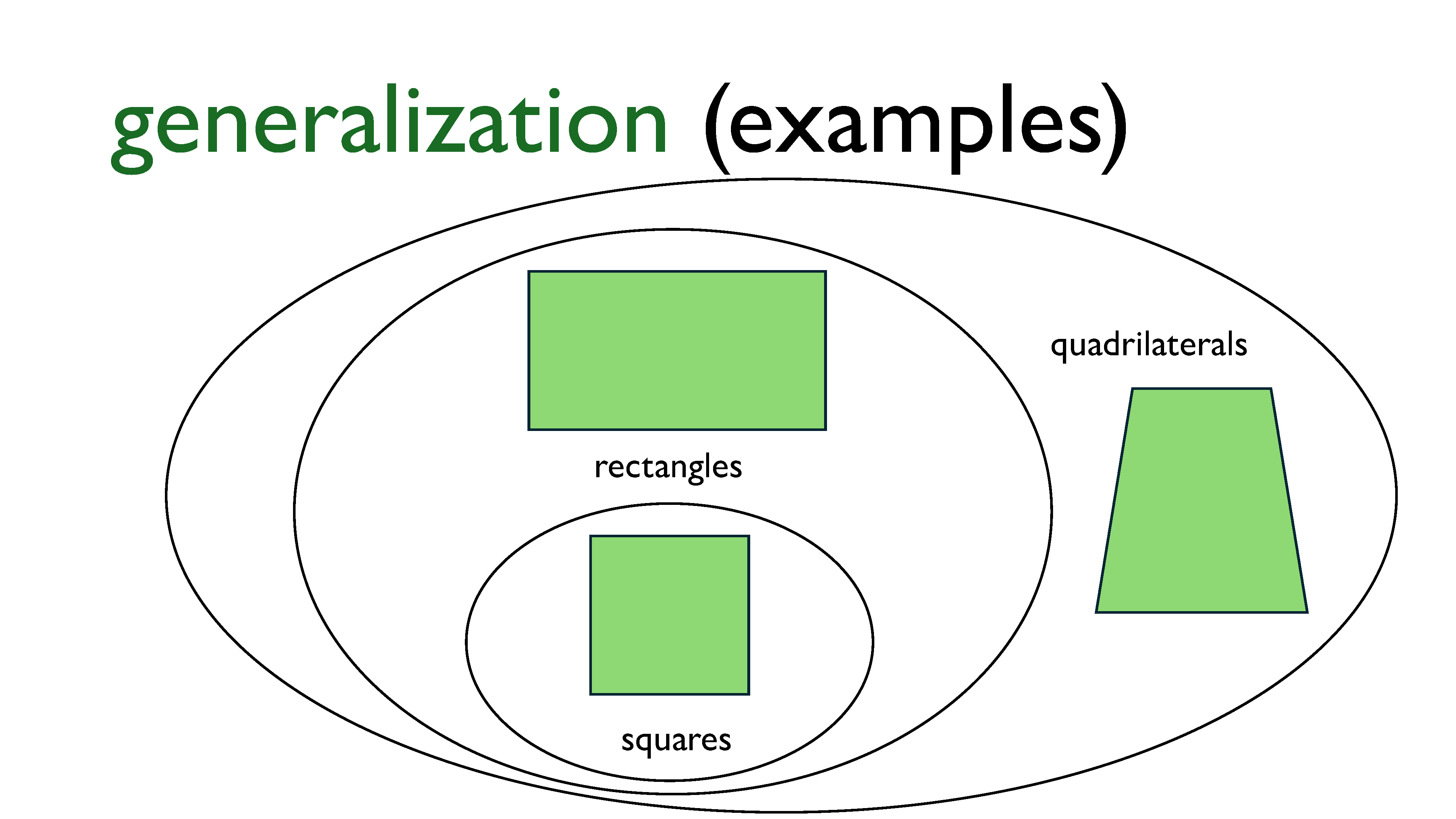
An example of generalization is this idea of classifying polygons. One way to classify them is based on the number of sides they have, the lengths of the sides, and their angles. As we can see in the slide, a square is a rectangle, which is a quadrilateral. We could extend this more: squares and rectangles are both trapezoids, and then we could have trapezoids that don’t have any symmetry, and lastly, quadrilaterals.
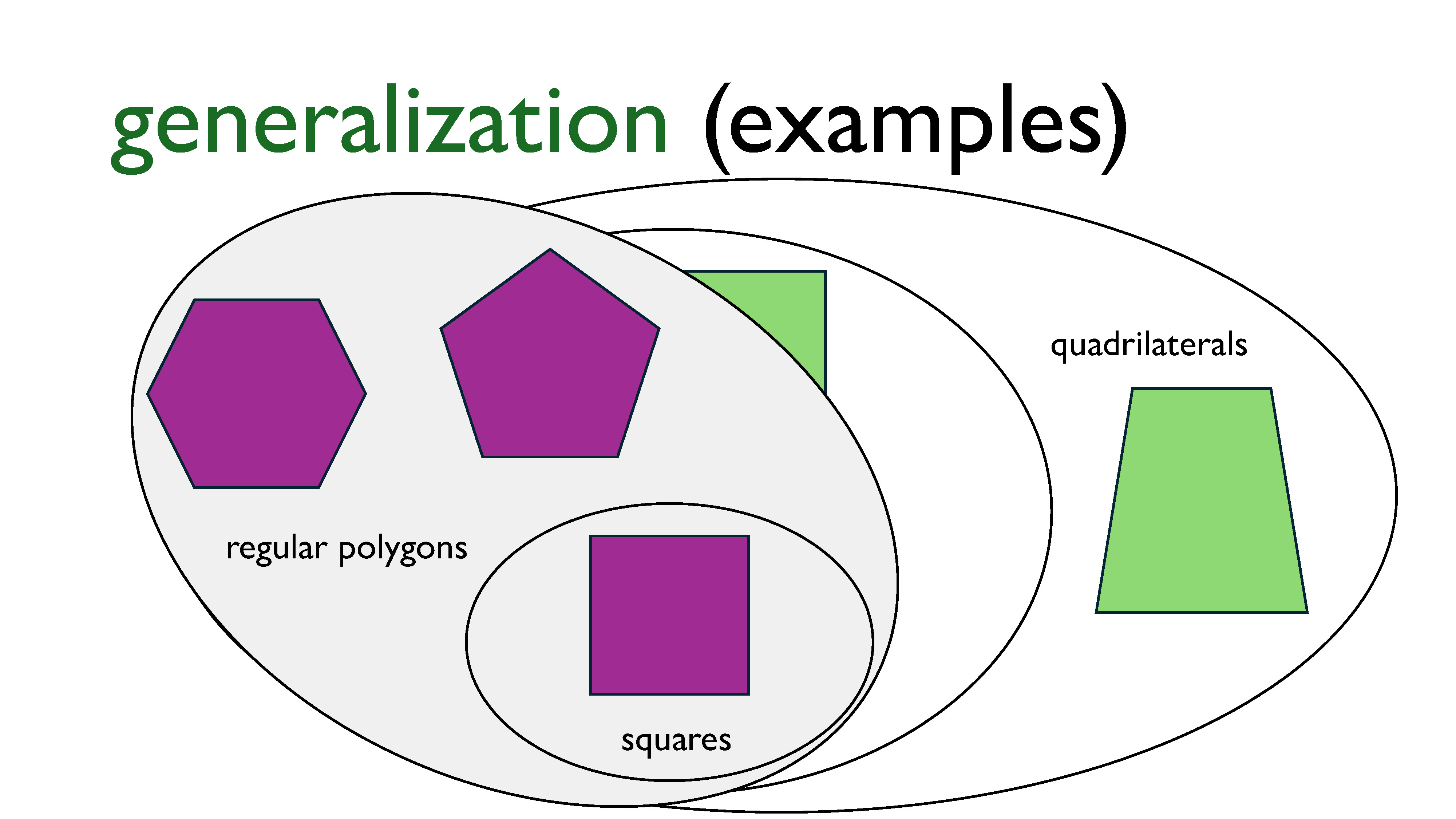
But squares are also regular polygons! So another way of classifying shapes might be to more coarsely separate them into regular polygons and irregular polygons, or even have some sort of category for polygons that have some symmetry to them but aren’t quite regular.

We also see the idea of generalization a lot in biology, especially when it comes to classifications. Taxonomy is all about classifying species into hierarchical classes of groups with shared characteristics, using a defined and systematic process.
Theory $\neq$ Math!

The last thing I want to say as part of this “defining theory” section is that contrary to popular opinion, mathematicians do not have a monopoly on theory. There are lots of ways to use theoretical tools and approaches without ever dealing with math, and lots of them are useful in computer science! Being able to break down and understand problems and ideas is a universally applicable skill that manifests itself in lots of different ways.
However, math is often useful in theoretical contexts, especially when the problems being tackled, or the questions being studied, are of a quantitative nature. This is because math is a very precise language for describing problems, and also abstracts away a lot of (at times irrelevant) qualitative details. This can be very helpful when trying to come up with generalized solutions to problems. But please do note that I never said mathematical language was clear. Contrary to what your math professors might tell you, mathematical language is often very unclear and can be difficult. But it is precise, and that precision can be key.

So where are we going with this? I know I just said that theory is not synonymous with math, but as it happens, I am going to be talking about math today. That’s just because the problem I’ve been studying for the past several months is very mathematical in nature, and I want to use it as a case study. I want to provide an example of how the ideas I’ve just discussed might be actually used in computer science, and give you an idea of why math-adjacent courses (like a course in discrete math, or a course in algorithms, for instance) shouldn’t be written off as a waste of time.
For the rest of this talk, I’m going to go up and down the ladder of abstraction to show you why we do theory, and concretely show you how it is useful.
First, we’re going to look at some real-world problems. We’re going to precisely describe these problems using math, and we’re going to look at some solutions for these problems. Then, we’re going to see how generalizing these solutions can give us solutions to some related problems for free.
And that, right there, is the power of theory.
Part 2 of this talk is now available here!