Hypergraph Theory Basics
An informal introduction
Graphs can be seen as a way to represent pairwise relationships between objects. With graphs, we have one object type and one relationship type. In one of the most common canonical applications of graph theory, social networking, we are trying to understand and represent social groups using graphs. In that case, our object is people, our pairwise relationship is friendship, and two people have a relationship between them if they are friends.
When we draw a graph, the primary objects are typically represented as dots or small circles, which we call vertices, and a relationship between two objects is indicated by putting a line between the two vertices that represent them. We call these lines edges.
Hypergraphs are easier to look at as a way to represent one to many relationships between objects. Here, we can consider the relationships to involve a primary object (the “one”) and a secondary object (the “many”). For example, if we consider our primary object to be people, and our secondary object to be movies, then we can consider our relationship to be a person liking some group of movies. Each primary object is related to an arbitrary number of secondary objects.
In this case, our vertices are the secondary objects, and our hyperedges are the primary object. From here on out, we will refer to hyperedges as “edges” for the sake of simplicity.
As you might have noticed, this informal definition of a hypergraph allows empty edges (someone might dislike all movies), and it also allows multiple or repeated edges (someone might like exactly the same set of movies as someone else). The definition of a hypergraph does not allow repeated edges, and typically we don’t consider empty edges either.
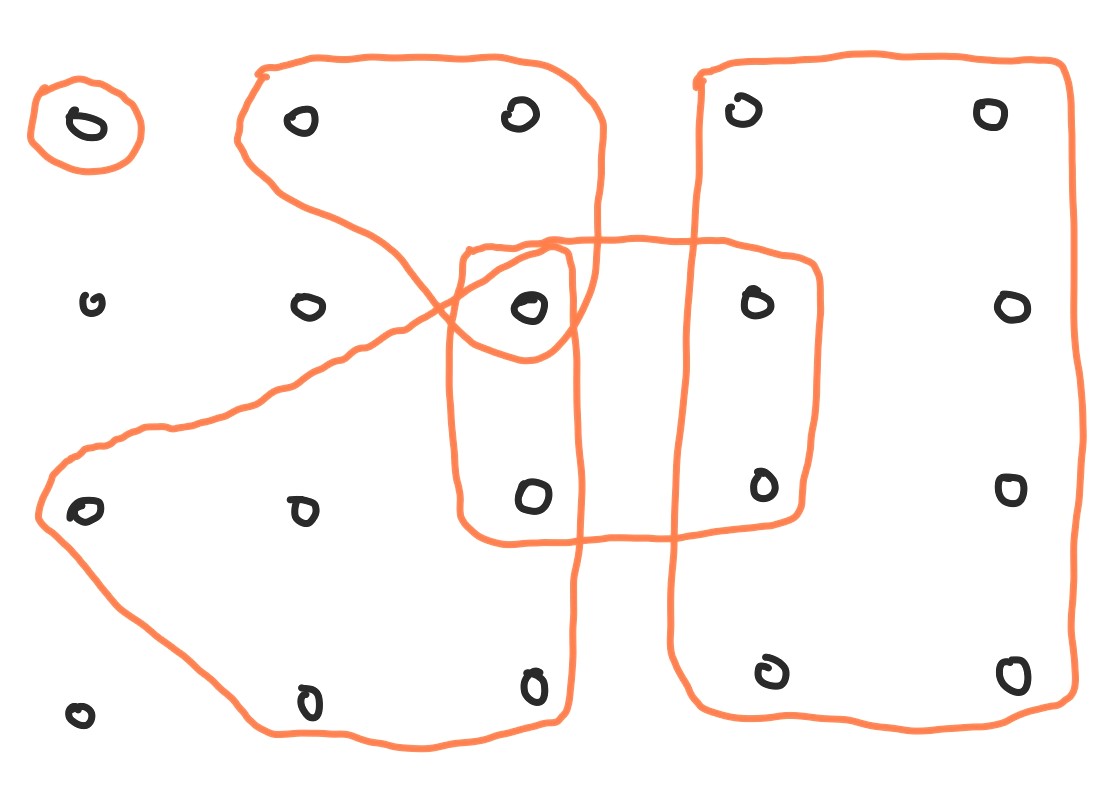
It can be helpful to visualize a hypergraph as a pegboard with elastics around different groups of pegs, as shown in the image above. In that case the primary objects are the elastics, the secondary objects are the pegs, and an elastic is related to a group of pegs if it is wrapped around them.
Some definitions
More formally, a hypergraph is a tuple $H = (V, E)$ where $V$ is a set and $E$ is a family of subsets of $V$: that is, $(E \subseteq \mathcal{P}(V))$. The number of vertices $n = |V|$ is called the order of a hypergraph, and the number of edges $m = |E|$ is called the size of a hypergraph.
An edge is called included if it is a subset of another edge in the hypergraph. An edge is called multiple or repeated if it contains the same vertex set as another edge in the hypergraph. All multiple and empty edges are also included edges.
An edge is called a loop if it only contains one vertex.
A hypergraph is called simple if it doesn’t contain any included edges or loops.
The rank $r(H)$ of a hypergraph is the number of nodes in the edge with the most nodes, or the maximum cardinality of an edge in $H$.
The anti-rank or co-rank of a hypergraph (denoted $cr(H)$) is the number of nodes in the edge with the least nodes, or the minimum cardinality of an edge in $H$.
A hypergraph $H$ is called k-regular if every vertex in $H$ has degree $k$, and k-uniform if $r(H) = cr(H) = k$ (every edge in $H$ contains $k$ vertices).
Note that under this definition, graphs are 2-uniform hypergraphs since their edge set can be written as $E \subseteq {e \in \mathcal{P}(V) : |e| = 2 }$
The maximum degree of a hypergraph $H$ is denoted $\Delta(H)$, and it is the degree of the vertex with the highest degree. (The degree of a vertex is the number of hyperedges that contain it).
Hypergraph representations
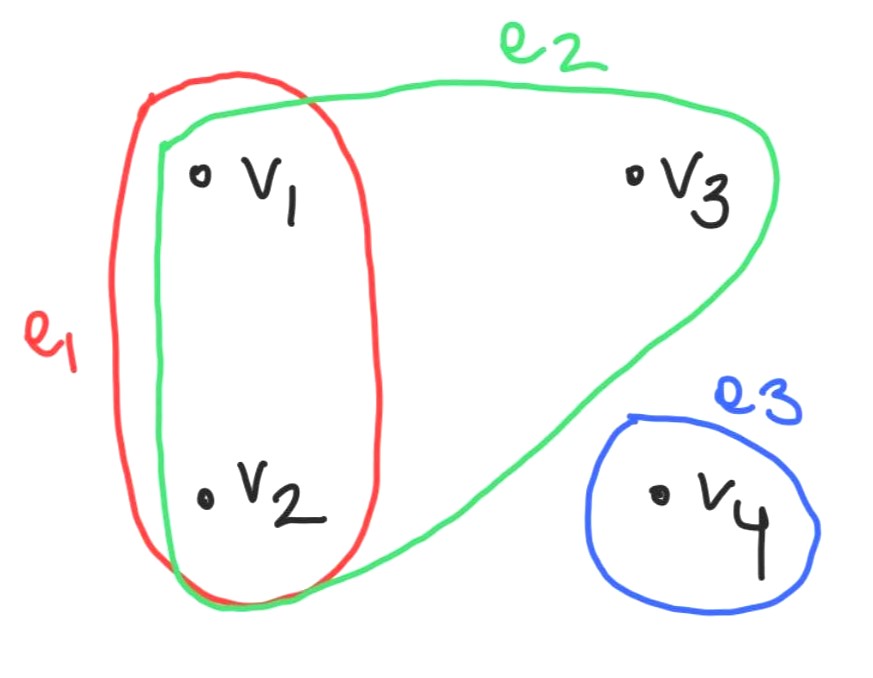
The easiest way to represent a hypergraph is to draw the nodes as labelled points, and draw curves around them, which represent edges. For example, below is a drawing of $H = (V, E)$ where $V = {v_1, v_2, v_3, v_4}$ and $E = {e_1:{v_1, v_2}, e_2:{v_1, v_2, v_3}, e_3:{v_4} }.$
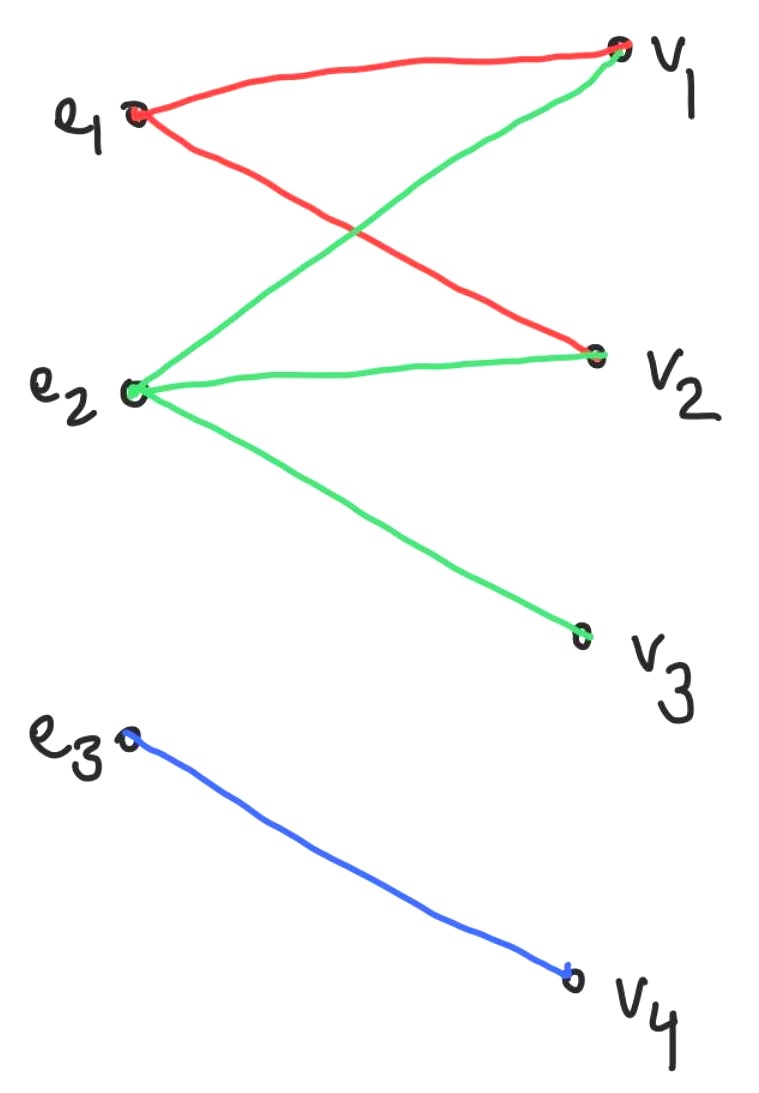
Hypergraphs can also be represented using incidence matrices and incidence graphs. As shown in the figure below, in an incidence graph, we represent both vertices and hyperedges as nodes in the new graph, and put an edge between an edge node and a vertex node if the edge contains that vertex.
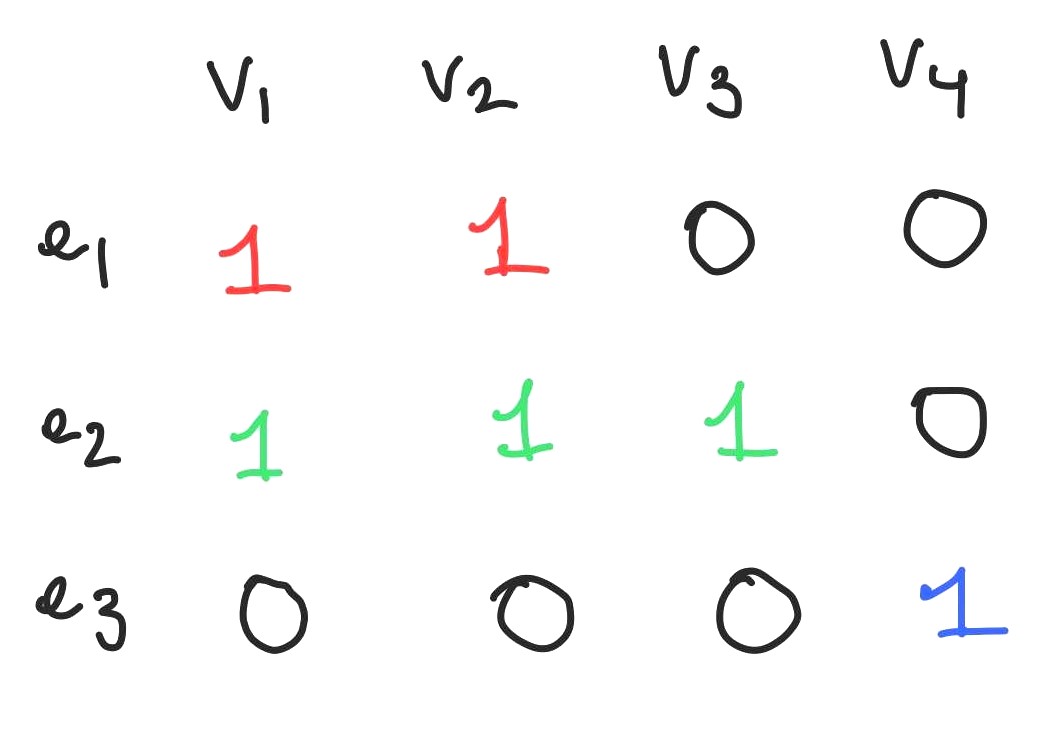
In an incidence matrix, each row represents an edge and each column represents a vertex, giving us an $m \times n$ matrix. We enter the number 1 in row $i$, column $j$ of the matrix if $e_i$ contains $v_j$, and enter 0 otherwise. This representation is very useful because it allows us to do things like computing the cardinalities of edges (row sums) and the degrees of vertices (column sums) much more systematically. You can see an example of an incidence matrix below.
Multi-hypergraphs
A further generalization of a hypergraph is a multi-hypergraph, where we allow multiple edges to share the same vertex set. These are defined as a triple $H = (V, E, \textrm{supp})$ where $V$ is a set of vertices, $E$ is a set of edges, and the support function $\textrm{supp} : E \rightarrow \mathcal{P}(V)$ maps individual edges to subsets of the vertex set.
This definition becomes very natural from the point of linear algebra, because then we can look at an edge as being a row in an $m \times n$ matrix where all entries are either 0 or 1 (and any matrix over ${0,1}$ can be represented in this way).
This definition also allows us to model one to many relationships more effectively, since now we are able to map two different entities to the exact same group of objects. However, in practice, weights are often added to edges to indicate their multiplicity or level of importance, since it is a more condensed representation than having repeated edges.
Dual Hypergraphs
Informally, the dual of a hypergraph (or multi-hypergraph) $H$ is a hypergraph where we transform all edges of $H$ into vertices in the new hypergraph, and all vertices of $H$ into edges in the new hypergraph.
Formally, let’s consider a hypergraph $H = (V,E)$ of order $n$ and size $m$. The dual hypergraph $H^* = (V^*, E^*)$ is a hypergraph of order $m$ and size $n$. We define its vertex set as being equal to the edge set in the original hypergraph, $(V^* = E)$ and we define its edge family $E^*$ as the family of sets $x_1, x_2, … x_n$ where $x_i$ is the set of all edges in $E$ incident to $v_i$ in $H$.
The dual $H^* = (V^*, E^*, \textrm{supp}_{H^*})$ of a multi-hypergraph $H = (V, E, \textrm{supp})$ can be defined in a similar fashion by way of the support function.
Note: the incidence graph of $H^*$ is isomorphic to the incidence graph of $H$ (its dual), and the incidence matrix of $H^*$ is the transpose of the incidence matrix of $H$. The dual of a regular hypergraph is uniform, and the dual of a uniform hypergraph is regular.